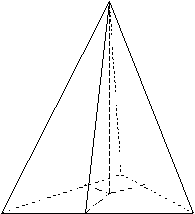
1.Вершина тетраэдра проектируется в центр вписанной окружности.
Центр вписанной окружности в равнобедренном треугольнике АВС – это точка пересечения высот, медиан, биссектрис.
КВ – медиана, биссектриса, высота она равна а*
6.Неопределённость решения может возникнуть в связи с различным положением ортогональной плоскости на некоторую плоскость одной или нескольких точек заданной фигуры. Например, если плоскости боковых граней тетраэдра составляют с плоскостью основания равные углы, то вершина этого тетраэдра может проектироваться как в центр вписанной в основание окружности, так и в центры вневписанных окружностей.
Задача 6.
В основании тетраэдра, все плоскости боковых граней которого наклонены к плоскости основания под углом А, лежит правильный треугольник со стороной а. Найти объём тетраэдра.Решение:
Возможно два случая:
|
|
1.Вершина тетраэдра проектируется в центр вписанной окружности. Центр вписанной окружности в равнобедренном треугольнике АВС – это точка пересечения высот, медиан, биссектрис. КВ – медиана, биссектриса, высота она равна а* |
Объём V = 1/3*Sосн*Н. КН = а
/6, т.к. медиана делится 2 : 1 считая от вершины.
Угол DКН – это угол А, именно под углом А каждая грань наклонена к основанию. DH = а
/4.
Oбъем пирамиды V = a
3 * tg А /24.
 |
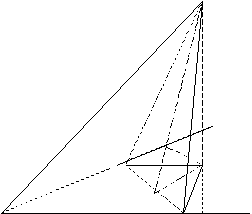2.Если вершина тетраэдра проектируется в центр вневписанной окружности. Центр вневписанной окружности- лежит на пересечении биссектрис двух внешних углов треугольника АВС (продолжение двух любых сторон треугольника). Внешний угол равностороннего треугольника равен 120 0 . |
Треугольник ВСН – равносторонний треугольник, найду HD.
HD = a/2*tgA; S
/4.
Объём тетраэдра равен V= a3/8*tgA.