Задача 3. В основании прямой призмы лежит ромб со стороной а и острым углом А. Через сторону основания проведена секущая плоскость под углом В к плоскости основания. Найти площадь сечения, если высота призмы равна h?

• tgB > h/(a sinА)
• tgB < h/(a sinA)
• tgB = h/(a sinA)

Рассматриваю именно эти случаи неопределённости т.к. сторона сечение в прямой призме может падать на плоскость A₁B₁C₁D₁, B₁BC₁C и на сторону В₁С₁.

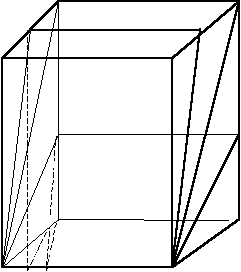1.tgB > h/(a* sinА) - сечение AMND(а это параллелограмм). Площадь параллелограмма равна S = a*ha. Построю линейный угол двугранного угла В, это угол угол ОКМ. Т.К. треугольник МКО прямоугольный и КО = a*sinA,то MK(ha)=h/sinB. Отсюда следует что S(AMND)=a*h/sinB.

2. tg B< h/a*sinA – сечение AM₁N₁D(это параллелограмм). S=a*h_a. Линейный угол двугранного угла В – М₁К₁В, т.к. треугольник М₁К₁В – прямоугольный и К₁В = a*sinA, то М₁К₁ = a* sinA/cosB. Отсюда следует S_(AM1N1D) = a²*sinA/cosB.

3. tgB = h/a*sinA – сечение АВ₁С₁D(это параллелограмм). S=a*h_a. Линейный угол двугранного угла В – В₁К₂В, т.к. треугольник В₁К₂В прямоугольный и В₁К₂ = a* sinA:

• В₁К₂ = h/ sinB, отсюда следует S = a*h/sinB