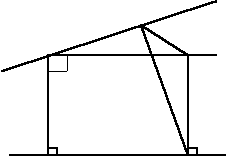
Через точку С проведем прямую l параллельно прямой n. Через эти две прямые проведём плоскость, построим отрезок BE параллельно CD, тогда угол АВЕ равен искомому.
2.Неопределённость условия может возникнуть в связи с произвольным выбором заданных или искомых точек. Точка может находиться внутри или вне отрезка; точка или несколько точек могут принадлежать и не принадлежать фигуре, принадлежать одной или нескольким плоскостям
Задача 2.
Угол между двумя скрещивающимися прямыми равен 60 0. Точка А лежит на одной прямой, точка В - на другой, причем расстояние от этих точек до общего перпендикуляра равны расстоянию между скрещивающимися прямыми. Найти угол между общим перпендикуляром прямых и прямой АВ.Возможно два случая:
Решение:
Пусть m и n скрещивающиеся прямые, CD - их общий перпендикуляр.
 |
Точка А принадлежит прямой m
расположена вправо от точки С.
Через точку С проведем прямую l параллельно прямой n. Через эти две прямые проведём плоскость, построим отрезок BE параллельно CD, тогда угол АВЕ равен искомому. |
Найдем его:
треугольник АВЕ прямоугольный ВЕ перпендикулярно СЕ;
ВЕ перпендикулярно m, то перпендикулярна к (АCЕ) значит и ко всем прямым
лежащим на этой плоскости АЕ перпендикулярна ВЕ, а по условию АЕ=ВЕ
![]() Угол АВЕ=45
0
Угол АВЕ=45
0
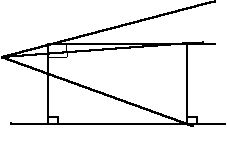 |
2)Точка А расположена влево от точки С.
Обозначим её А1.
|