Рассмотрим наиболее
типичные случаи неопределенности
1.Часто в условии задачи не указан вид треугольника в зависимости от угла, в то время как ответы для остроугольного, прямоугольного и тупоугольного треугольника могут быть различными.
Задача 1.
Угол между медианой и биссектрисой проведенными из одной вершины равен A, а между этой биссектрисой и высотой, выходящей из той же вершины, равен В. Какой угол больше: А или В ?Решение:
 |
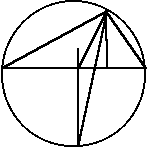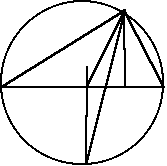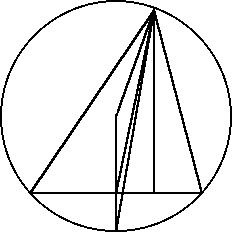
Опишем около треугольника АВС окружность и продолжим биссектрису AL угла ВАС до пересечения с окружностью в точке D. Радиус OD будет перпендикулярен стороне ВС, которую он пересекает в точке М, причем СМ = МВ. Н - основание высоты, проведенной из вершины А. Отрезок МД параллелен отрезку АН, то угол MDA = углу LAH. |
Возможны три случая:
1).Угол ВАС< 90>0, значит треугольник АВС - остроугольный, тогда АМ
(медиана) > OA(радиус) >MD(отрезка);
т.е. в треугольнике AMD против большей стороны лежит больший угол
угол А<угла В
 |
2)Угол ВАС>900
треугольник АВС -
тупоугольный, угол ВАС>900;
тогда АМ < OA < MD,
т.е. АМ < MD |
 |
3)Угол ВАС=900
треугольник АВС - прямоугольный,
угол ВАС=900; тогда АМ=ОА=MD
т.е. треугольник АМD равн-ный AM=MD |
угол А > угла В.
угол А = углу В.